رگرسيون و همبستگی چندگانه

آخرین به‌روزرسانی: 24 دی 1401

در این فصل به آموزش رگرسیون و همبستگی چندگانه، در ادامه سری مقالات آموزشی آمار به زبان ساده می پردازیم.

مقدمه ای بر تحلیل چند متغیره

تا این بخش كار همبستگی به صورت میان دو متغیر مورد بررسی قرار گرفت. در حالی كه علاوه بر آن می توان همبستگی را میان سه و یا تعداد بیشتری متغیر مطرح كرد؛ به عنوان مثال میان سطح استعداد (IQ)، نمرات مدرسه و نمرات دانشگاهی در مقابل عملكرد شغلی. تحلیل چند متغیره به معنای بررسی چند متغیر به صورت همزمان است.

در این فصل به بررسی رگرسیون و همبستگی با بیش از دو متغیر پرداخته می شود كه مسئله ای قابل توجه است زیرا اغلب مجموعه ای از داده ها و عوامل در كنار هم بررسی شده(مانند پرسشنامه یا یک پیمایش) و علاقه مند به سنجش میزان ارتباط آن ها هستیم. به عنوان مثال ممكن است بخواهیم میزان ارتباط میان كیفیت مسكن، تراكم مسكن، شبکه های حمایت اجتماعی و آلودگی هوا بر سلامت را محاسبه كنیم.

همبستگی جزئی

در فصل قبل مثال هایی جهت بررسی معنی داری ارتباط میان زمان مطالعه و عملكرد آزمون ارائه شد. ممكن است بخواهیم اثر متغیر سومی، به عنوان مثال سطح هوش را در همبستگی در نظر بگیریم. در صورتیكه متغیر هوش با متغیر زمان مطالعه همبستگی مثبتی داشته باشد بدین معنی است كه دانشجویان هوشمند تر بیشترین زمان را صرف مطالعه می كنند، همچنین، چنانچه هوش با عملكرد آزمون ارتباط مثبتی داشته باشد به معنای این است كه دانشجویان باهوش تر نمرات بالاتری را در آزمون دریافت می كنند.

بنابراین همبستگی میان زمان مطالعه و عملکرد آزمون به سادگی ممکن است تحت تأثیر عامل سومی تحت عنوان هوش قرار گیرد. در مواردی مشابه این حالت، به دلیل وجود همبستگی میان هر کدام از عوامل مورد بررسی با عامل هوش، ممکن است رابطه ی بدست آمده میان زمان مطالعه و عملکرد آزمون حقیقی و قابل اطمینان نباشد. بدین معنی که دانشجویان باهوش تر هم مدت زمان بیشتری صرف مطالعه کرده و هم نمرات بالاتری در امتحان دریافت می کنند. اگر اثر هوش حذف شود، رابطه ی زمان مطالعه به عملکرد آزمون ممکن است مخدوش شود.

باید توجه داشت كه همبستگی بیانگر علی بودن یك رابطه نیست. به عنوان مثال ممكن است تعداد خانه های ساخته شده در یك دوره یكساله ارتباط مثبتی با میزان آلودگی شهر داشته باشد. در صورتیكه ادعا كنیم خانه ها سبب آلودگی هستند و یا آلودگی بیشتر در نتیجه ی ساختمان های بیشتر منتج می شود، برداشتی اشتباه داشته ایم. در این حال احتمال می رود كه همبستگی متأثر از عامل سومی چون جمعیت باشد كه با هر دو عامل ذكر شده در بالا رابطه داشته باشد. تعداد خانه ها و همچنین، آلودگی بیشتر شاید نتیجه ی افزایش جمعیت (و فعالیت های بشری) باشد. همبستگی میان خانه ها و آلودگی به سادگی تحت تأثیر عامل سومی بوده كه به اندازه ی خود سهم مهمی در همبستگی دارد.

جهت پاسخ به سؤال میزان اثر هوش روی همبستگی زمان مطالعه و عملكرد آزمون نیاز است همبستگی متغیر زمان مطالعه و عملكرد آزمون پس از برطرف کردن اثر هوش مورد آزمون قرار گیرد. در صورتیكه همبستگی مخدوش شود دلالت بر ناشی شدن آن از عامل سوم دارد. این كار با استفاده از همبستگی جزئی انجام می پذیرد. در مرحله ی اول می بایست میزان همبستگی عامل هوش با زمان مطالعه و عملكرد آزمون به صورت جداگانه محاسبه شود. جهت انجام این كار میزان هوش دانشجویان با برگزاری آزمونی اندازه گیری شده است. نتایج حاصل از این آزمون به همراه زمان مطالعه و نمره آزمون در جدول زیر نمایش داده شده است.

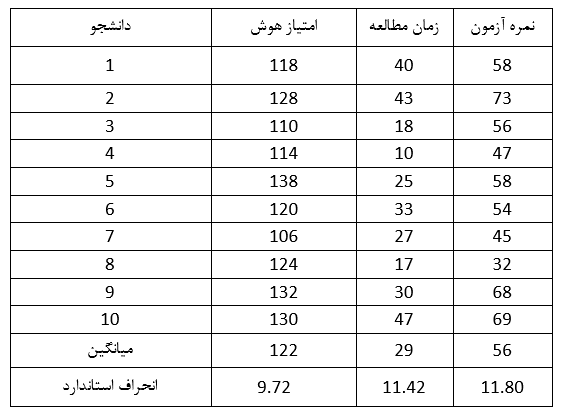
با استفاده از روش های ذكر شده در این فصل ضرایب همبستگی زیر محاسبه خواهند شد:

زمان مطالعه و عملكرد آزمون r = 0.72

زمان مطالعه و هوش r = 0.37

عملكرد آزمون و هوش r = 0.48

همبستگی ها نشان می دهند كه هوش رابطه ی مثبتی با دو متغیر دیگر دارد و همین امر دلیل ادامه ی بررسی ها است.

فصل قبل را به یاد بیاورید كه در آن رگرسیون اجازه ی پیش بینی یك متغیر را با استفاده از متغیر دوم می داد. در صورتیكه بین زمان مطالعه و هوش رابطه ی رگرسیونی برقرار شود با داشتن زمان مطالعه می توان به پیش بینی میزان هوش پرداخت. بنابراین تفاوت مقادیر واقعی زمان مطالعه و پیش بینی هایی كه توسط رگرسیون بدست می آیند در واقع همان مقادیر زمان مطالعه پس از حذف اثر عامل هوش هستند.

به این تفاوت ها در این قسمت به جای خطا، اصطلاح باقیمانده ها اطلاق می شود؛ زیرا اصطلاح خطا زمانی به کار می رود عامل هوش توانایی لازم برای پیش بینی زمان مطالعه را ندارد، اما در این مورد این مقدار همان شاخصی است که به دنبال آن هستیم و در واقع مقداری است که پس از حذف اثر هوش در متغیر زمان مطالعه باقیمانده است. (در واقع تغییرات باقیمانده در نمرات)

با برازش رگرسیون زمان مطالعه به هوش معادله ی زیر به دست می آید:

24.50- هوش *0.044 = زمان مطالعه

اكنون با داشتن این رگرسیون مقادیر پیش بینی شده ی زمان مطالعه بدست آمده و پس از تفاضل آنها از مقادیر واقعی باقیمانده ها را خواهیم داشت. جدول زیر نشان دهنده ی این امر است (به تذكر 19 توجه داشته باشید).

با این كار اثر هوش از زمان مطالعه حذف می شود. اكنون نیاز است اثر هوش را از عملكرد آزمون حذف کنیم كه مشابه حالت قبل ابتدا رگرسیونی میان عملكرد آزمون و هوش برازش داده و معادله ی زیر را خواهیم داشت:

15.60-هوش * 0.59 = عملکرد آزمون

در این مورد از این معادله رگرسیونی جهت استخراج باقیمانده ها در عملكرد آزمون استفاده می شود.

اكنون قادریم همبستگی باقیمانده های متغیر زمان مطالعه را با باقیمانده های نمرات آزمون، در حالیكه اثر هوش از هر دو عامل حذف شده است، بدست آوریم. همبستگی مقادیر بدست آمده r برابر با 0.665 نتیجه می دهد كه به دلیل اینكه ارتباط متغیر زمان مطالعه و عملکرد آزمون را با در نظر گرفتن اثر هوش در مدل بدست آورده، آن را همبستگی جزئی نامند.

در مورد این مثال مشاهده می شود كه مقدار همبستگی كاهش یافته است اما هنوز معنی دار است (در p = 0.05)، و نتیجه می شود كه همبستگی اصلی تنها در اثر سومین عامل یعنی هوش ایجاد نشده است و ملاحظه می شود كه پس از در نظر گرفتن اثر هوش، باز هم رابطه ی معنی داری میان مقدار زمان صرف شده جهت مطالعه و عملكرد آزمون وجود دارد.

آنچه را كه تاكنون انجام داده ایم می توان با نمایشی از تغییرات مقادیر هر كدام از متغیرها در دایره ای نشان داد. چنانكه در شكل 21.1 مشاهده می شود سه دایره با هم همپوشانی دارند. قسمت SE+SIE بخشی از تغییرات متعلق به عملكرد آزمون توضیح داده شده توسط زمان مطالعه را در بر دارد، قسمت SI+SIE مربوط به زمان مطالعه توضیح داده شده توسط هوش و IE+SIE سهم عملكرد آزمون تبیین شده توسط هوش را پوشش می دهد.

اندازه ی این ناحیه ها را با محاسبه ی r^2 هر كدام از همبستگی های مرتبط می توان بدست آورد. زمانی كه اثر هوش حذف می شود در واقع بخشی از دایره كه در آن عامل هوش باشد (I+SI+SIE+IE) از قسمت مربوط به تغییرات زمان مطالعه یعنی S+SE و همچنین، تغییرات مربوط به عملكرد آزمون برابر با E+SE كم می شود. همبستگی جزئی زمان مطالعه و عملكرد آزمون با برطرف کردن اثر هوش ما را به ناحیه ی SE به عنوان تغییرات باقیمانده از عملکرد آزمون که توسط تغییرات باقیمانده از زمان مطالعه توضیح داده شده اند، هدایت می کند.

خوشبختانه زمانی كه ضرایب همبستگی مربوط به كلیه متغیرها را به صورت جداگانه داشته باشیم، روشی ساده تر جهت محاسبه همبستگی جزئی وجود دارد كه در آن دیگر نیازی به یافتن باقیمانده ها نیست. جهت راحتی كار و گسترش تعداد متغیرها به جای X و Y، آنها را با شماره های 1 ، 2 و 3 نامگذاری می كنیم. كه در مورد مثال ذكر شده عملكرد آزمون را 1، زمان مطالعه را 2 و هوش را 3 نامگذاری می كنیم.

قابل ذكر است كه این فرمول حاوی ضرایب همبستگی جزئی با حذف اثر متغیر 3 می باشد. با ادامه دادن چنین منطقی می توان اثر متغیرهای 5 ، 6 و غیره را برطرف کرد. چنانچه دقت شود این فرمول فرضی كلیدی در دل خود دارد و آن همبستگی خطی متغیرهای 1 و 2 است. مدل خطی قابل بسط به كلیه ی متغیرها است. در صورت معتبر نبودن چنین فرضی نمی توان اثر كلیه ی متغیرهای مورد نظر را تعدیل کرد و تنها متغیرهایی كه رابطه خطی آنها برقرار باشد در محاسبه همبستگی جزئی قابلیت تعدیل شدن را دارند.

همبستگی چند متغیره

از همبستگی جزئی جهت محاسبه ی همبستگی چند متغیره استفاده می شود و در واقع ضریب همبستگی چند متغیره ،یعنی R بیانگر چگونگی ارتباط سه متغیر یا بیشتر با یكدیگر است. در این قسمت تغییراتی در زمینه ی روش نامگذاری وجود دارد كه در ادامه بیان خواهند شد. بدین صورت كه متغیری خاص را در نظر گرفته و آن را Y یعنی متغیر وابسته نامیده و میزان و چگونگی ارتباط آن با متغیرهای باقیمانده سنجیده می شود. (همچنانكه در بخش های بعد در بحث رگرسیون چند متغیره خواهیم دید) Y متغیری است كه اغلب علاقه مند به پیش بینی آن هستیم.

درمورد مثال مورد بررسی فرض كنیم علاقه مند به پیش بینی مقادیر عملكرد آزمون باشیم. بنابراین سایر متغیرها را 1 ، 2 ، 3 و…. می نامیم. كه در مورد این مثال فقط دو متغیر دیگر یعنی زمان مطالعه و هوش باقی می مانند كه به ترتیب متغیرهای 1 و 2 نامیده می شوند.

جهت سهولت توضیح دادن، به جای R با توان دوی ضریب همبستگی یعنی R^2 ، به نشانه ی ضریب تعیین همبستگی چند متغیره كار خواهیم كرد. هر کدام از متغیرهای 1 ، 2 ، 3 و غیره را به نوبه خود می توان انتخاب کرده و بخشی از تغییرات متغیر Y را که توسط هر کدام از آنها توضیح داده می شود و توسط سایر متغیرهای پیشین تبیین نشده است را بدست آورد. چنانچه این مقادیر با هم جمع شوند، معیاری از میزان تغییرات توضیح داده شده متغیر Y توسط ترکیبی از سایر متغیرها را ارائه می دهد.

همبستگی چند متغیره هستند. مشکل استفاده از این راه این است که در صورت اضافه شدن هر متغیر می بایست تغییرات Y از آن حذف شود که باعث طولانی تر شدن فرمول می شود. در هر صورت باید توجه داشت که در صورت اضافه شدن متغیر خطر افزایش همبستگی با علل تصادفی و نه به خاطر وجود روابط حقیقی افزایش خواهد یافت.

بنابراین زمانی که تعداد زیادی از متغیرها به عنوان پیش بینی کننده وجود دارند می بایست در محاسبه ی همبستگی چند متغیره توجه بیشتری داشت و به نوعی افزایش نادرست ایجاد شده توسط متغیرهای اضافه شده را جبران کرد. (برنامه های کامپیوتری آماری مانند SPSS برای این کار مقداری با عنوان “ضریب همبستگی تعدیل شده”را ارائه داده اند- هینتون و دیگران. 2004 را ببینید.)

رگرسیون چند متغیره

رگرسیون خطی را برای بیش از دو متغیر می توان انجام داد. در این بخش نیاز است به نامگذاری متغیرها بپردازیم. متغیر وابسته را Y نامیده و سایر متغیرها، متغیرهای مستقل و یا پیش بین هستند که در پیش بینی Y به کار می روند. به جای آنچه در رگرسیون خطی یک متغیره داشتیم در این بخش با تعدادی از متغیرها شامل X1, X2, . . . , Xk در رگرسیون مواجهیم که در آن k تعداد متغیرهای پیش بین است. جهت بدست آوردن رگرسیون خطی می بایست معادله ی خطی زیر را محاسبه کرد:

رگرسیون خطی را برای بیش از دو متغیر می توان انجام داد. در این بخش نیاز است به نامگذاری متغیرها بپردازیم. متغیر وابسته را Y نامیده و سایر متغیرها، متغیرهای مستقل و یا پیش بین هستند که در پیش بینی Y به کار می روند. به جای آنچه در رگرسیون خطی یک متغیره داشتیم در این بخش با تعدادی از متغیرها شامل X1, X2, . . . , Xk در رگرسیون مواجهیم که در آن k تعداد متغیرهای پیش بین است. جهت بدست آوردن رگرسیون خطی می بایست معادله ی خطی زیر را محاسبه کرد:

در نهایت ضریب a محاسبه می شود:

A=56-(0.65X29)-(0.30X122)=0.55

پس از تكمیل محاسبات معادله ی رگرسیون چند متغیره به صورت زیر خواهد بود:

Y’=0.55+0.65X1+0.3X2

با جایگزینی اسامی واقعی متغیرها فرمول پیش بینی عملكرد آزمون با استفاده از عوامل زمان مطالعه و هوش پدیدار خواهد شد:

هوش 0.30+ زمان مطالعه 0.65+0.55 = نمره آزمون

با استفاده از این فرمول قادر به پیش بینی مقادیر خواهیم بود، به عنوان مثال دانشجویی با سطح هوشی برابر با 110 كه در هر هفته 30 ساعت مطالعه می كند در آزمون نمره ای برابر با زیر بدست خواهد آورد:

53.35 = (110*0.30) + (30* 0.65) + 0.55= نمره آزمون

بنابراین بر اساس رگرسیون خطی چند متغیره پیش بینی می شود كه دانشجویی نمره ای برابر با 53.05 را دریافت كند.

همخطی چندگانه

زمانی كه متغیرهای پیش بین همبستگی بالایی با یكدیگر داشته باشند در اصطلاح گفته می شود كه همخطی چندگانه وجود دارد و در صورت وجود آن در رگرسیون چند متغیره احتمال ایجاد مشكل وجود دارد. اولین مشكل به دلیل توضیح دادن مشابه تغییرات متغیر وابسته Y توسط تعداد زیادی از متغیرهای پیش بین است. حالتی كه در آن دو متغیر پیش بین وجود دارد را در نظر بگیرد.

زمانی كه دو متغیر وابسته نباشند در آن صورت تغییرات توضیح داده شده از متغیر وابسته Y توسط اولین متغیر با دیگر متغیر متفاوت است در حالیكه اگر همبستگی میان متغیرهای پیش بین وجود داشته باشد، نوعی همپوشانی در توضیحات داده شده از Y توسط آنها وجود دارد. دومین مشكل مشخص نبودن ترتیب اهمیت تغییرات توضیح داده شده توسط متغیرهای پیش بین است خصوصاً زمانی كه تعداد متغیرهای پیش بین زیاد باشد رخداد این مشكل امری بدیهی است.

تركیب متغیرها تحت یك متغیر و یا حذف آن، در صورتیكه دقیقاً پیش بینی ای مشابه با متغیر دیگر دارد از جمله روشهای رویارویی با مشكل همخطی چندگانه است. به عنوان مثال تصور كنید كه می خواهید قد فردی را با توجه به سایر مشخصه های بدن مانند طول پا، طول ساعد، شاخص طول انگشت او و … تقریب بزنید. اگر طول پای چپ و راست هر دو به عنوان متغیرهای جداگانه در نظر گرفته شوند، ممكن است همبستگی نسبتاً بالایی نسبت به یكدیگر داشته و نیازی به حضور هر دوی آنها كه منجر به همخطی چندگانه می شود، نباشد و باید در مورد انتخاب فقط پای راست و یا پای چپ و یا حتی میانگینی از هر دو پا تصمیم گیری شود.

محاسبه رگرسیون چند متغیره

در مورد مثال ذكر شده كلیه ی متغیرهای پیش بین در رگرسیون شركت دارند و البته جای تعجب نیست زیرا فقط دو متغیر وجود داشته و این عمل رگرسیون مستقیم نامیده می شود. روشی جهت انجام رگرسیون زمانی كه متغیرهای پیش بین بیشتری وجود داشته باشد، كار كردن با معادلات با استفاده از متغیرهای پیش بینی است كه همبستگی بالایی با متغیر وابسته داشته باشند. پس از آن متغیرهای پیش بین بر اساس میزان حداكثر واریانسی كه توضیح می دهند به ترتیب به مدل اضافه می شوند. این فرآیند پس از اینكه متغیری وجود نداشته باشد كه میزان R² را به طور معنی داری افزایش دهد، پایان می پذیرد.

این روش را رگرسیون پیشرو گویند. روش دیگری وجود دارد كه در آن ابتدا كلیه متغیرهای پیش بین وارد مدل شده و پس از آن هر مرتبه متغیری كه كمترین مشاركت را در R² داشته باشد حذف می شود، تا زمانیكه دیگر متغیرهایی كه مقدار R² را به طور معنی داری کاهش می دهند حذف شوند و آن نقطه بخش پایانی رگرسیون است.

این روش رگرسیون پسرو نامیده می شود. رگرسیون قدم به قدم دو روش ذكر شده در بالا را با هم تركیب می كند به گونه ای كه به طور همزمان متغیره ها را اضافه و یا كم می كند. دلیل استفاده از انواعی از روشها به جای روش مستقیم این است كه در بیشتر رگرسیون هایی كه جهت پیش بینی بكار می روند، تعداد كمی از متغیرها بخش زیادی از تغییرات متغیر وابسته را توضیح داده و تبیین می كنند؛ و این كار علاوه بر اینكه باعث صرفه جویی در زمان و محاسبات می شود، متغیرهایی را كه كمترین میزان شركت در پیش بینی را دارند از گردش كار حذف می كند.

جهت مشاهده جزئیات بیشتر در ارتباط با چگونگی محاسبه ی همبستگی و رگرسیون چند متغیره با استفاده از نرم افزار آماری SPSS به فصل 16كتاب هینتون و دیگران (2004) مراجعه شود.

در مقاله بعدی به بخش دوم رگرسیون و همبستگی خطی پرداختیم.

مترجمین: دکتر هدی کامرانی فر – حسن اسکندری نیا