اثر متقابل عوامل در آناليز واريانس

آخرین به‌روزرسانی: 24 دی 1401

در فصل سیزدهم مقاله آموزشی آمار به زبان ساده به آنالیز واریانس یک عاملی با اندازه گیری های مکرر پرداختیم. در این فصل به آموزش اثر متقابل عوامل در آنالیز واریانس در ادامه سری مقالات آموزشی آمار به زبان ساده می پردازیم.

اغلب محققین معمولاً علاقه مند به بررسی اثرات بیش از یك متغیر مستقل هستند تا اینكه بخواهند آنها را به صورت جداگانه مورد مطالعه قرار دهند، به عنوان مثال اثرات متغیرهای سن و جنس بر روی عملكرد رانندگی در بزرگراه. خوشبختانه آنالیز واریانس این قابلیت را دارد كه بیش از یك متغیر مستقل را به كار گیرد. در واقع یك آنالیز واریانس می تواند هر تعدادی از متغیرهای مستقل را مورد بررسی قرار داد و تنها مسئله تحلیل نتایج پیچیده آن است.

به هر حال همانطور كه مشاهده می شود آنالیز واریانس دو عاملی مزیت های قابل توجهی را در مطالعه دو متغیر مستقل به صورت جداگانه به همراه دارد، خصوصاً به عنوان یك طرح دو عاملی به ما اجازه ی آزمون اثرات متقابل دو متغیر مستقل را در نمرات می دهد. در این فصل به اهمیت اثرات متقابل در آنالیز داده ها پی خواهیم برد. این امر توسط مثال هایی كه در ادامه خواهند آمد توضیح داده خواهد شد.

گزارشی به كمیته ی آموزش و پرورش ارجاع داده شده بود كه مدرسه ای در شهر (مدرسه ای قدیمی) به دلیل دلسرد كردن دختران از مطالعه علوم معروف شده است و به محققی مأموریت بررسی این مسئله داده شد. همچنین، محقق مدرسه ای دیگر (مدرسه ای جدید) كه از نظر تعداد موضوعات مورد بررسی بر روی شاگردان (و تعدادی از سایر عامل های مفید مانند اندازه، استانداردها، سن تدریس، نسبت پسران به دختران و غیره جهت كنترل عوامل اختلاط گر) مطابقت داشت انتخاب شد.

ماكسیمم سن برای دانش آموزان مورد مطالعه در این شهر پانزده سال در نظر گرفته شد و البته این سن زمانی است كه وسیع ترین طیف موضوعات جهت بررسی وجود دارد. محقق به صورت تصادفی تعداد 20 تا از پسران و 20 تا از دختران پانزده ساله از هر مدرسه انتخاب كرده تا چگونگی ارتباط مهارت های علمی كه انتخاب شده بودند را دریابد. در این آزمایش دو متغیر مستقل وجود دارد، مدرسه و جنسیت، و متغیر وابسته ی اندازه گیری شده تعداد مهارت های علمی منتخب در نظر گرفته شد.

در این تحقیق محقق علاقه مند به بررسی اثرات متغیرهای مستقل به صورت جداگانه نبوده و به تركیبی از دو متغیر پرداخته می شود، به عنوان مثال آیا با در نظر داشتن تعداد موضوعات علمی انتخابی اختلاف معنی داری میان دختران و پسران در مدرسه ی قدیمی نسبت به مدرسه ی جدید وجود دارد؟ آنالیز واریانس با دو عامل راهی برای پاسخ دادن به این سوال است.

آنالیز واریانس دو عاملی سه نسبت واریانس به جای یك نسبت ایجاد می كند. دو نسبت اول مربوط به بخش اثرات اصلی دو عامل است، بدین معنی كه هر عامل را هم به صورت جداگانه در نظر گرفته و هم اثر آن روی متغیر وابسته بررسی کرده است.اثر اصلی “مدرسه” بیانگر این است که آیا اختلاف معنی داری میان تعداد موضوعات علمی منتخب در مدرسه قدیمی در مقایسه با مدرسه جدید وجود دارد (که در واقع ترکیبی از نمرات پسران و دختران در هر مدرسه است).

در این حال همانطور که علاقمندیم بیان می کند که کدام مدرسه علم گراتر است ولی اطلاعی از تفاوت های میان پسران و دختران نمی دهد. اثر اصلی جنسیت بیان می کند که آیا تفاوت معنی داری میان پسران و دختران با در نظر گرفتن تعداد موضوعات انتخابی وجود دارد. که در این حال پسران از هر دو مدرسه و دختران دو مدرسه با هم ترکیب می شوند. که مانند حالت قبل اطلاعاتی از تفاوت در موضوعات علمی انتخابی بر اساس جنسیت می دهد اما از چگونگی تفاوت میان دو مدرسه اطلاعی نمی دهد.

بررسی وجود اثر متقابل میان عوامل از سایر موارد دیگری است که یک آنالیز واریانس دو عاملی می دهد. اثر متقابل معنی دار زمانی رخ می دهد که اثر یک عامل در سطوح مختلف عامل دیگر متفاوت باشد. بنابراین اثر مدرسه بر روی انتخاب موضوعات علمی در پسران متفاوت از همین اثر در دختران می باشد. اگر مدرسه اثری روی پسران نداشته باشد، در هر مدرسه ای که تحصیل می کردند تفاوتی بین تعداد موضوعات علمی منتخب وجود نداشت.

اما اگر اثر مدرسه روی دختران معنی دار باشد، دختران مدرسه ی قدیمی مهارت های علمی کمتری نسبت به دختران مدرسه ی جدید دارند؛ بنابراین اثر متقابل در فرض آزمایشی مورد بررسی ایجاد می شود. در این حال اثر مدرسه در سطوح جنسیت متفاوت است. رسم نمودار میانگین برای سطوح مختلف بهترین شیوه جهت آگاهی از وجود اثر متقابل است همچنانکه در نمودار 14.1 نشان داده شده است، که آنچه را که در ارتباط با اثر متقابل ذکر شد به تصویر کشیده است.

باید توجه داشت چنانچه اثر متقابل بدست آمده که در نمودار 14.1 نشان داده شده است معنی دار باشد به طور یقین می توان گفت که دلیل آن متفاوت بودن مهارت های علمی مدرسه قدیمی در مقایسه با مدرسه جدید است و به دنبال آن اثر اصلی مدرسه معنی دار می شود، همچنین، اگرچه پسران مهارت های علمی بیشتری نسبت به دختران داشته باشند ولی چون اثرات اصلی فقط تشکیل دهنده ی بخشی از اثر متقابل هستند، خود به تنهایی تعیین کننده ی نتایج مهم نخواهند بود. اثر متقابل بدست آمده به روشنی بیان می دارد که در مدرسه ی قدیمی دختران مهارت های علمی کمتری نسبت به پسران دارند در حالیکه در مدرسه ی جدید چنین تفاوتی وجود ندارد.

در صورتی كه تفاوت پسران و دختران (دختر-پسر، پسر منهای دختر) در مدرسه ی قدیمی نسبت به مدرسه ی جدید بیشتر باشد، حتی اگر پسران نسبت به دختران در مدرسه ی جدید مهارت های علمی بیشتری كسب می كردند، نتیجه فرض آزمایشی همچنان پابرجاست.

در اینجا اثر متقابل نشاندهنده ی تفاوت معنی دار میان دو مدرسه در اثر جنسیت با در نظر گرفتن مهارت علمی انتخابی است.

اثرات متقابل

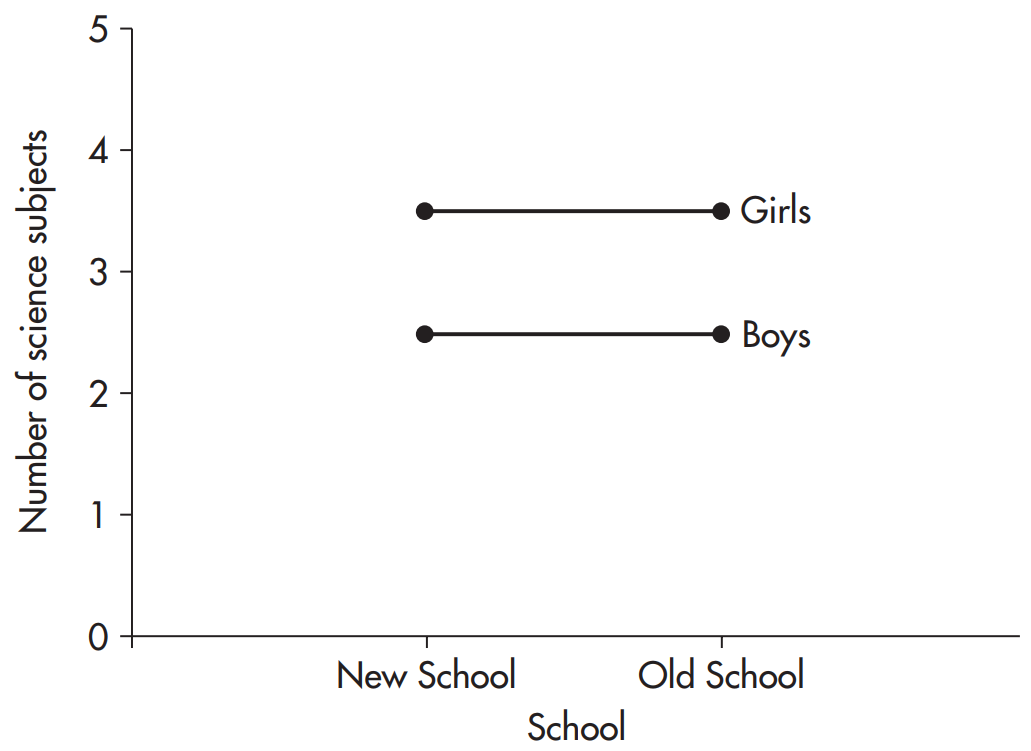
زمانی كه اثر یك عامل در عاملی دیگر جمع پذیر[1] باشد نتایج حصولی دربردارنده ی اثر متقابل نخواهند بود. به داده های مثال مطالعه مدرسه در نمودار 14.2(الف) توجه كنید. در اینجا اثر جنسیت معنی دار شده است (مشاهده می كنیم كه دختران مهارت های علمی بیشتری نسبت به پسران كسب كرده اند) در حالیكه اثر اصلی مدرسه معنی دار نشده است (مهارت های علمی كسب شده در هر دو مدرسه یكسان است). بدین معنی كه هر كدام از مدرسه ها را كه انتخاب كنیم اثر جنسیت مشابه است و میزان مهارت های علمی با تغییر از پسر به دختر میانگین یكسانی دارد.

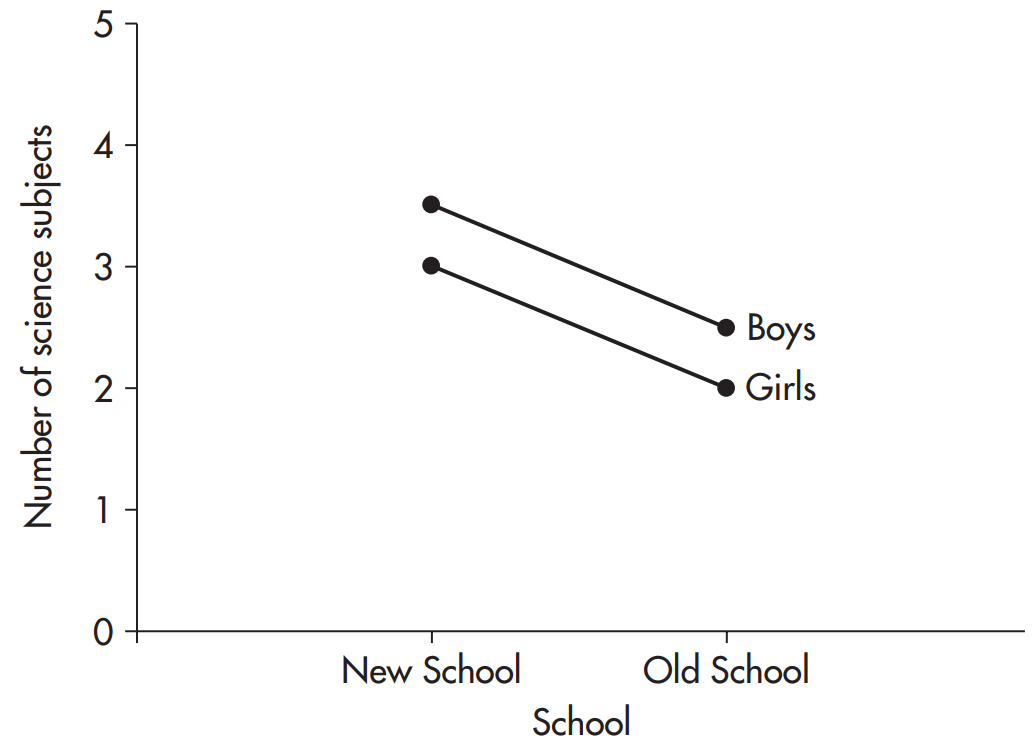
اثر اصلی مدرسه در مثال داده های نمودار 14.2(ب) وجود دارد و مهارت های علمی كسب شده در مدرسه ی جدید بیشتر است و به همین ترتیب در مورد اثر اصلی جنسیت، بدین معنی كه پسران مهارت های علمی بیشتری نسبت به دختران كسب می كنند. اما با وجود این اثرات اصلی از نمودار 14.2(ب) دریافت می شود كه اثر متقابلی وجود ندارد. تفاضل میانگین نمرات پسران با دختران در هر دو مدرسه به میزان 0.5 تغییر می كند. به طور مشابه صرف نظر از اینكه در هر دو مدرسه نمرات پسران را در نظر بگیریم یا نمرات دختران را، تفاضل میانگین نمرات مدرسه قدیمی و جدید در یك مجموعه ی برابر یا یك تغییر می كند.

با توجه به نمودار میانگین های دو عامل آزمایشی می توان گفت زمانی كه خطوط در نمودار موازی باشند، اثرمتقابلی وجود ندارد و چنانچه نمایش داده می شود اثرات عوامل جمع پذیر هستند. مثال های نمودار های 14.2(ج) و 14.2(د) چون خطوط موازی نیستند به طور واضح نمی توان گفت كه جمع پذیر هستند.

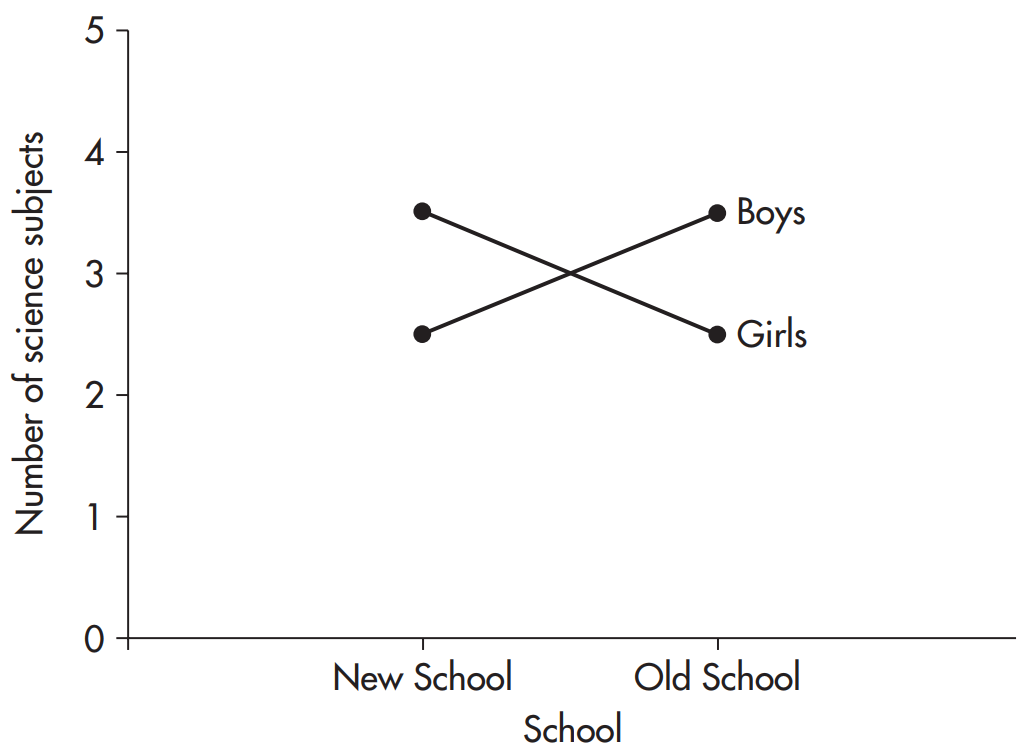
در این موارد اثر متقابل وجود دارد و می توان گفت كه اثر آن در دو آنالیز واریانس دو عاملی معنی دار است. نمودار 14.2(ج) شامل اثر اصلی نمی باشد اما اثر متقابل نشان می دهد كه اثر اصلی جنسیت از یك مدرسه به مدرسه ی دیگر به صورت معكوس تغییر می كند. در مدرسه ی قدیمی پسران مهارت های علمی بیشتری نسبت به دختران كسب می كنند درحالیكه در مدرسه ی جدید این دختران هستند كه مهارت های علمی بیشتری نسبت به پسران كسب می كنند.

در نمودار 14.2(د) علاوه بر آنكه اثر متقابل وجود دارد فاصله ی نسبتاً زیادی بین تفاضل پسران و دختران (پسر منهای دختر) در مدرسه ی قدیمی نسبت به مدرسه ی جدید وجود دارد. همچنین، چون در حالت كلی پسران مهارت های علمی بیشتری دارند اثر اصلی جنسیت معنی دار است، اما اثر اصلی مدرسه در این مثال معنی دار نیست.

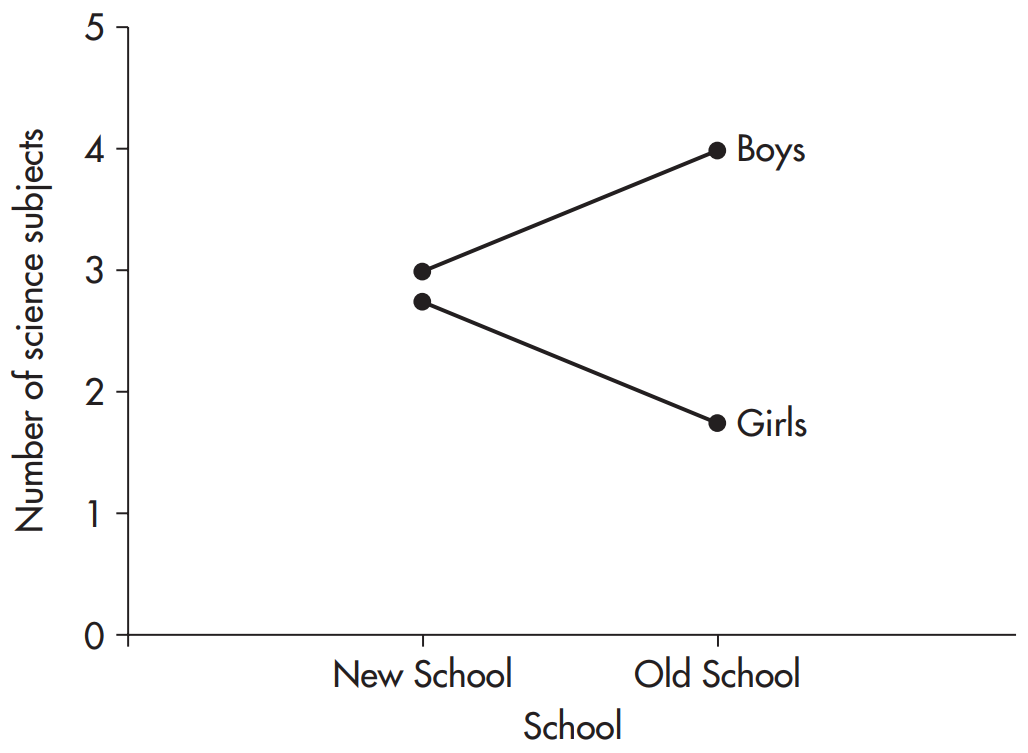
مثال های بالا مثال های جامع و کاملی نیستند اما صرف نظر از تعداد بسیار زیاد سطوحی که می توان داشت قوانین اساسی بدین صورت حکم می کنند: خطوط موازی نمایانگر جمع پذیری عوامل هستند که در آن صورت اثر متقابلی وجود ندارد. زمانی که خطوط موازی نباشند اثر متقابل وجود داشته که نشاندهنده ی (در صورتیکه معنی دار باشد) اثر متفاوت یکی از عوامل در سطوح متفاوت عامل دیگر است.

تقسیم کردن مجموع مربعات بین سطوح

در آنالیز واریانس یک عاملی دیده ایم كه تغییر پذیری فقط بین سطوح وجود دارد و دربردارنده تغییرات سیستماتیك بین سطوح است. تنها جمله ی خطا در این زمان ایجاد می شود و زمانی كه اندازه گیری های تكرار شده را در مقابل مقادیر اندازه گیری شده مستقل به كار می بریم، تغییر می كند. مشابه آن را برای آنالیز واریانس دو عاملی داریم. اما در مورد آنالیز واریانس دو عاملی تغییرات دوره ای از سه منبع حاصل می شوند: اثر عامل اول (آن را عامل A می نامیم، مانند مدرسه)، اثر دومین عامل (عامل B نامیده می شود، مانند جنسیت) و اثر متقابل دو عامل (عامل A×B نامیده می شود).

همچنانكه قادریم مجموع كل مربعات را به دو بخش تقسیم بندی كنیم: مجموع مربعات بین گروهی و مجموع مربعات درون گروهی، قادر خواهیم بود مجموع مربعات بین گروهی را به مجموع مربعات ناشی از عامل A، عامل B و عامل A×B تقیسم كنیم. به یاد بیاورید كه مجموع مربعات از رابطه ی زیر محاسبه می شد:

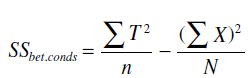
كه از مجموع كل برای محاسبه تغییرات نمرات بین سطوح استفاده می كند. اگر از این فرمول در طرح دو عاملی استفاده می كردیم، تفاوت بین سطوح معنی دار می شد اما خود عامل های سازنده این تغییرات معنی دار نبودند. در مثال ما، با وجود 20 آزمودنی (n=20)، چهار سطح داریم: مدرسه ی قدیمی و پسران، مدرسه ی قدیمی و دختران، مدرسه ی جدید و پسران، مدرسه ی جدید و دختران.

فرض كنید در حال حاضر فقط علاقه مند به عامل A (مدرسه) هستیم. بنابراین سطوحش را با عامل B برای تولید سطوح A به تنهایی تركیب می كنیم: برای به دست آوردن عامل اصلی A، مدرسه ی قدیمی (A1) و مدرسه ی جدید (A2)، سطح پسران و مدرسه ی قدیمی را با دختران و مدرسه ی قدیمی و همچنین، پسران و مدرسه ی جدید را با دختران و مدرسه ی جدید تركیب می كنیم. مجموع مربعات عامل A را به صورت زیر می توان محاسبه كرد:

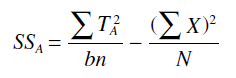
این فرمول از مجموع كل سطوح عامل A (در مورد این مثال و) و bn، تعداد كل نمرات در هر كدام از سطوح عامل A، و b تعداد سطوح عامل B (در مورد این مثال دو تا وجود دارد: پسران و دختران). حاصل تركیب 20 مورد پسران و مدرسه ی قدیمی و 20 مورد دختران و مدرسه ی قدیمی 40 (bn) آزمودنی در مدرسه ی قدیمی است. میانگین مربعات با استفاده از درجه آزادی عامل A (a-1، كه تعداد سطوح عامل A است و در این مثال برابر با 2 است).

به طور مشابه برای عامل B با تركیب سطوح B درون سطوح عامل A می توان روند مشابهی را انجام داد. برای تولید سطح B1، پسران، حالت پسران و مدرسه ی قدیمی را با پسران و مدرسه جدید تركیب می كنیم و جهت تولید B2، دختران، حالت دختران و مدرسه ی قدیمی را با دختران و مدرسه ی جدید تركیب می كنیم. و در نهایت فرمول محاسبه مجموع مربعات عامل B به صورت زیر نتیجه می شود:

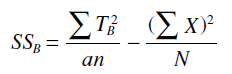
چنانچه فرمول بالا را بر درجه آزادی (b-1) تقسیم كنیم مجموع مربعات عامل B حاصل می شود.

اكنون می توان اثر متقابل مجموع مربعات را محاسبه كرد. از آنجایی كه علاقه مند به تغییرات كلی سطوح عامل A و عامل B تحت عنوان سطوح AB هستیم، كلیه ی سطوح را با هم تركیب می كنیم. در مورد مثالی كه ذكر شد حالت های پسران و مدرسه ی قدیمی (A1B1)، دختران و مدرسه ی قدیمی (A1B2)، پسران و مدرسه ی جدید (A2B1)،دختران و مدرسه ی جدید (A2B2). در ادامه مجموع مربعات به صورت زیر به دست می آید:

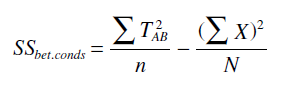
توجه داشته باشید كه آنچه كه در بالا آمده است همان فرمول مجموع مربعات بین گروهی است. تنها تفاوت در برچسب گذاری است: مربوط به كل سطوح است كه به جای آن می توان T یا به كار برد. سطح اول A1B1 است، سطح دوم A1B2، سطح سوم A2B1و سطح چهارم A2B2 نام دارند و كلیه ی تغییر پذیری نمرات ناشی از عوامل A، B و عامل اثر متقابل A×B را در بر می گیرند. اكنون می توان مجموع مربعات عامل A و B را از آن كم كرد و آنچه باقی می ماند اثر متقابل خواهد بود.

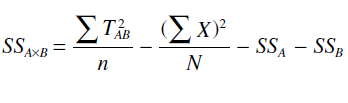
با تقسیم كردن بر درجه آزادی اثر متقابل، (a-1)(b-1) میانگین مربعات اثر متقابل نتیجه خواهد شد.

اكنون جهت محاسبه آماره ی F برای سه عامل نیاز است واریانس های خطا را برای مقایسه با میانگین مربعات پیدا كنیم. انتخاب میانگین مربعات خطا وابسته به این است كه بدانیم آیا عوامل مستقل هستند یا مقادیر اندازه گیری شده ی تكرار شده می باشند كه در فصل آینده در زمینه چگونگی انجام آن شرح خواهیم داد.

اثرات ساده ی اصلی

چنانچه در یك مجموعه از داده ها اثر متقابل معنی دار شود بدین معنی است كه یكی از عوامل اثری متفاوت در سطوح فاكتوری دیگر دارد. در مورد مدرسه ی مثال ما اثر متقابل به معنی متفاوت بودن اثر مدرسه در پسران نسبت به همین اثر در دختران است. چنانچه علاقه مند باشیم می توان از مسیرهای دیگر به همین نتیجه رسید: اثر جنسیت در مدرسه ی قدیمی در مقایسه با مدرسه ی جدید متفاوت است.

با توجه به اینكه به نوع علاقه مندی ما راههای متفاوتی جهت بررسی اثر متقابل وجود دارد. در حال حاضر از طریق اثر جنسیت به این مهم می پردازیم و می خواهیم بررسی كنیم كه آّیا تفاوتی میان پسران و دختران در مدرسه ی قدیمی وجود دارد و چگونگی مقایسه ی آن با تفاوت پسران و دختران در مدرسه ی جدید را بررسی كنیم.

به دنبال شناسایی اثر متقابل می توان اثرات ساده ی اصلی یك عامل را در سطوح عامل دوم مورد توجه قرار داد. محاسبه اثرات ساده ی اصلی مشابه انجام آنالیز واریانس یك عامل در هر كدام از سطوح عامل دوم است. در مورد مثال ذكر شده می توان اثرات ساده اصلی جنسیت روی مدرسه ی قدیمی و اثرات ساده اصلی جنسیت بر روی مدرسه ی جدید را بدست آورد. هنگامی كه اثرات ساده اصلی جنسیت روی مدرسه قدیمی مورد نظر است، نتایج مدرسه ی جدید را به طور كامل نادیده گرفته و روی مجموع مربعات میان سطح پسران و مدرسه ی قدیمی و سطح دختران و مدرسه ی قدیمی متمركز می شویم.

پس از آن می توان میانگین مربعات و مقدار آماره ی F را جهت مقایسه اثر ساده اصلی با جدول مناسب با آماره به كار برد. همین كار را برای اثر ساده اصلی جنسیت روی مدرسه ی جدید بدون توجه به نتایج مدرسه ی قدیمی می توان انجام داد. اگر اثر متقابل به صورت آنچه كه در نمودار 14.1 نمایش داده شد باشد، انتظار می رود كه اثر جنسیت در مدرسه ی قدیمی معنی دار باشد (چون دختران مهارت های عملی كمتری دارند) اما این اثر در مدرسه ی جدید معنی دار نیست (زیرا مهارت های علمی كسب شده توسط دختران و پسران متفاوت نیست). اثرات ساده اصلی فرض آزمایشی را قویاً حمایت می كنند.

اثرات ساده اصلی جنسیت در مدرسه ی قدیمی با مورد نظر قرارد دادن سطوح پسران و مدرسه ی قدیمی (A1B1) و دختران و مدرسه ی قدیمی (A1B2) قابل دستیابی است. باید توجه داشت كه تغییراتی در عامل B (جنسیت) میان دو سطح آن وجود دارد اما این تغییرات مربوط به عامل اصلی A نیست، بنابراین آنچه باقی می ماند سطح است و در نتیجه اثر تحت عنوان اثر ساده اصلی عامل B در سطح نامیده می شود. مجموع مربعات این اثر ساده اصلی از طریق فرمول زیر محاسبه می شود:

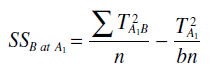
نتیجه گیری

آنالیز واریانس دو عاملی به ما اجازه ی آزمون كردن اثرات متقابل دو عامل را می دهد. اثرات اصلی هر عامل و اثر متقابل راهكاری جهت جداسازی مجموع مربعات بین سطوح به عناصر مجزا است. چنانچه بخواهیم به طور كاملتری به بررسی معنی دار بودن اثر متقابل بپردازیم می توانیم اثرات ساده اصلی یك عامل را در سطوح متفاوت عامل دیگر كه در یك زمان به دست آمده اند، بررسی كنیم. با این روش می توان به منبع اثر متقابل دست یافت.

[1] Additive

مترجمین: دکتر هدی کامرانی فر – حسن اسکندری نیا