مقدمه ای بر مدل خطی عام- بخش 2

آخرین به‌روزرسانی: 24 دی 1401

در ادامه مقاله  مقدمه ای بر مدل خطی عام، در اینجا به بخش دوم مدل خطی عام، در ادامه سری مقالات آموزشی آمار به زبان ساده می پردازیم.

تغییرات تبیین شده داده ها توسط مدل

در مثال ارائه شده، مدل خطی را یافتیم که بهترین برازش ممکن به داده ها را داشت و هیچ مدل خطی دیگری به اندازه مدل مطرح شده خوب نیست، چرا که ویژگی های ذکر شده برای باقیمانده ها در این مدل برقرار است. اکنون که بهترین مدل خطی را پیدا کردیم می توانیم دومین سؤال را بپرسیم: این مدل چقدر خوب و مناسب است؟ برای توضیح بیشتر این سؤال را دوباره به نحوی دیگر بیان می کنم: چه مقدار از اطلاعات موجود در داده ها توسط مدل تبیین شده و چه مقدار از آنها تبیین نشده و در قسمت خطا قرار گرفته اند؟ (توسط باقیمانده ها نشان داده می شوتد)

اگر به شکل 23.7 نگاه کنیم می بینیم که مدلی یکسان (خطی یکسان) به هر دو مجموعه داده برازش داده شده است (مجموعه اول با ضربدرها نشان داده شده است و دومی با نقطه). مشاهده می شود که علامت  های مثبت در مقایسه با علامت های به شکل نقطه در اطراف خط پراکندگی بیشتری دارند. می توان گفت که که باقیمانده ها برای مجموعه داده های اول بزرگتر از مجموعه دوم هستند. همچنین می توان گفت که برای مجموعه داده های اول بخش های تبیین نشده داده ها در مقایسه با مدل دوم بیشتر است.

لذا این مسئله ما را به این سو هدایت می کند که مدل دوم بهتر است. یک مدل خوب، تغییرات داده ها را به احتساب می آورد. از داده های مثال مطرح شده مشاهده می شود که با بزرگتر شدن کودکان نمرات دانش عمومی بالاتر می رود. مدل باید این مسئله را پیش بینی کند. برای بررسی مقدار اطلاعات تبیین شده از داده ها توسط مدل خطی دو روش مرتبط وجود دارد: همبستگی خطی و تحلیل واریانس. هر دو روش خطی بودن مدل را فرض می کنند، بنابراین جهت برقراری این شرط، پابرجا بودن فرضیات مطرح شده در مورد باقیمانده ها الزامیست.

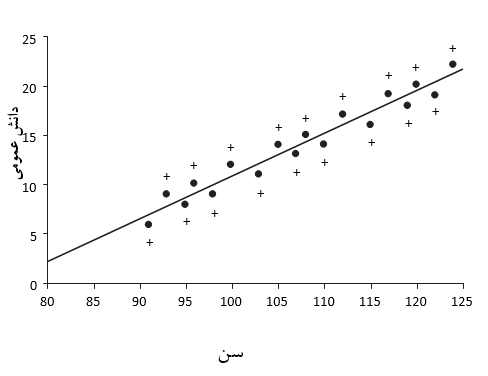
شکل 23.7- خطی یکسان برای دو مجموعه داده

مدل خطی و همبستگی

با بررسی ضریب همبستگی خطی می توانیم بررسی کنیم که آیا یک مدل خطی قادر است تغییرات زیادی را در داده ها تبیین کند یا فقط پوشش دهنده بخش کمی از آن است. این روش که از آن استفاده شده است (مطرح شده در فصل 20) تغییرات داده های اندازه گیری شده یک متغیر را در ارتباط با تغییرات متغیر دوم بررسی می کند. منتها این روش تنها با فرض خطی بودن رابطه بین این دو متغیر می تواند این کار را انجام دهد و سپس میزان قوی بودن رابطه را آزمون کند. این روش قابلیت تشخیص یک همبستگی غیر خطی پیچیده را ندارد و خیلی ساده در چنین حالاتی به ما ساده می گوید که داده ها از یک رابطه خطی بسیار بد پیروی می کنند. در مثال مطرح شده، همبستگی خطی نمرات دانش و سن با هم r=0.975 است که یک همبستگی بسیار زیاد است (01/0> p، برای یک پیش بینی دوطرفه، 16 = df). در حالت کل این شاخص بیان می دارد که با فرض خطی بودن رابطه، تغییرات در نمرات دانش عمومی نسب به تغییرات سن را تا حدود زیادی می توان محاسبه کرد.

به بیان ساده ، همبستگی خطی تحلیل زیر را انجام می دهد: با فرض وجود رابطه خطی بین متغیرها، چه مقدار از تغییرات در داده ها را می توان به آن رابطه نسبت داد و چه مقدار نمی تواند نسبت داده شود. با 95.1 درصد احتساب تغییرات موجود در داده ها، می توان اطمینان داشت که بین دو متغیر رابطه خطی وجود دارد.

مسئله جالب این است که ضریب همبستگی منطبق است با شیب “بهترین برازش” خط رگرسیونی نمرات z برای دانش عمومی و سن (جهت محاسبه در نمرات z در محاسبه همبستگی فصل 20 را ببینید).  نمره z یک نمره یا شاخص را استاندارد می کند به طوری که میانگین آن شاخص یا متغیر صفر و انحراف معیار آن 1 می شود. بنابراین به جای برقراری رگرسیون برای نمرات واقعی می توانیم خط رگرسیونی را به نمرات z برازش دهیم. با توجه به اینکه میانگین نمرات z صفر است لذا این خط از نقطه (0,0) عبور می کند و لذا  (مترجم: عرض از مبدأ) می شود. در این خط b=0.975 است که در واقع معادل همان r در شیب خط می باشد که در بخش های قبل به تفسیر بررسی شد.

برای نمرات z:   Zy=0+0.975z_x

بنابراین:  نمره z سن ×0.975=نمره z دانش عمومی

خوبی این مسئله این است که یک رابطه خطی قوی را نشان می دهد. با این حال، این فرمول در پیش بینی نمرات دانش عمومی از سن خیلی مفید نیست، زیرا بر اساس نمرات غیراصلی z بیان شده است، به همین دلیل اغلب از معادله رگرسیونی استاندارد استفاده می کنیم.

مدل خطی و تحلیل واریانس

جهت پاسخ داده به سوال بررسی میزان تغییرات تبیین شده داده ها  توسط مدل، می توان از تحلیل واریانس نیز استفاده نمود. روش تحلیل واریانس بر اساس فرض خطی بودن مدل ساخته شده است. تحلیل واریانس داده ها را با واریانس تبیین شده (توضیح داده شده) توسط مدل و واریانس توضیح ناپذیر (واریانس خطا) متناسب می کند. در  تحلیل واریانس به منظور اندازه گیری تغییرات نمرات دانش عمومی، بررسی فاصله نمرات از میانگین لحاظ می شود. در مثال فوق میانگین کلی نمرات دانش 14 است. اگر نمره فرزند اول برابر با 6 را در نظر بگیریم، پیش بینی مدل برای نمره کودک برابر با 6.98 است. بنابراین مدل می تواند مقدار 6.98-14=-7.02  از تغییرات نمره دانش آموز را براساس میانگین نمرات تبیین کند. سپس این اختلاف را به توان دو می رسانیم (این کار را همیشه انجام می دهیم تا هم مقدار اختلاف را اندازه بگیریم و همچین از علائم منفی ناخوشایند رها شویم). این مقدار برای دانش آموز اول برابر با 49.35 است. سرانجام ما این اختلافاتِ به توان دو رسیده را جمع می کنیم تا “مجموع مربعات”  برای مقدار تغییرات تبیین شده داده ها توسط مدل محاسبه شود. این ارقام در جدول زیر نشان داده شده است.

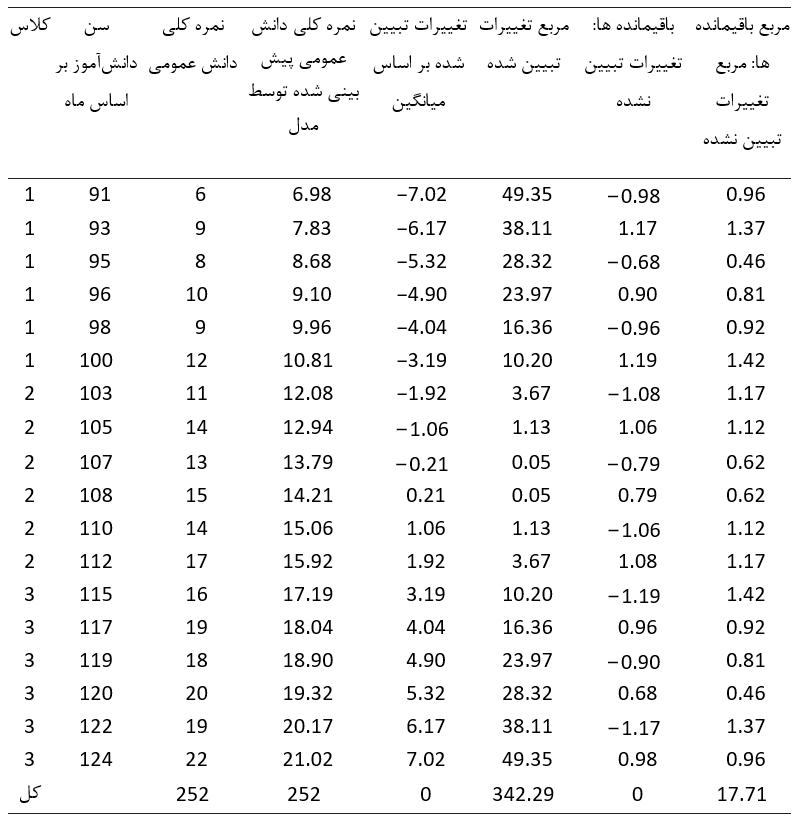
(من اعداد شش ستون را تا  دقت دو رقم اعشار آورده ام. اگر اعداد را فقط تا دو رقم اعشار جمع کنید، به دلیل خطای گرد کردن، مقدار 342.32 بدست می آورید.) در این مرحله دو مقدار “مجموع مربعات” نمرات دانش عمومی تبیین شده توسط سن (عدد  342.29) را با جمله “مجموع مربعات” خطا (مجموع مربعات خطا: 17و71) جمع می کنیم. بنابراین، از کل تغییرات موجود در داده ها (مجموع مجموع مربعات = 360.00) می توانیم 342.29 از آن را با استفاده از مدل خطی تبیین کنیم، و مقدار 17.71 بدون توضیح باقی می ماند. تکمیل یک جدول خلاصه تحلیل واریانس یا ANOVA یک مسئله ساده است – فقط می بایستی درجه های آزادی را ارائه دهیم تا محاسبات نهایی شود.

جدول خلاصه تحلیل واریانس

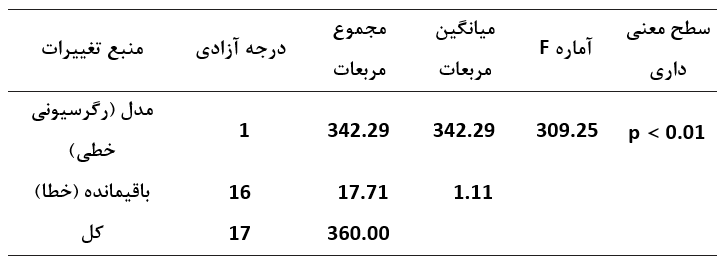
نتایج تحلیل واریانس به ما می گوید که مدل به طور قابل توجهی (سطح بالای معنی داری) می تواند تغییرات داده ها را تبیین کند.

در این کار از رگرسیون، همبستگی و تحلیل واریانس داده ها استفاده شده است. هر کدام از این تجزیه و تحلیل ها فرض می کنند که بین دو متغیر اندازه گیری شده رابطه خطی وجود دارد. در مثال بیان شده نیز سن و دانش عمومی، هر سه روش آماری مذکور فرض می کنند که رابطه خطی بین دو متغیر به قوت خود باقیست. با توجه به نتایج بدست آمده مشاهده می شود که این مدل خطی با داده ها مطابقت دارد و می تواند مقدار قابل توجهی از تغییرات نمرات را تبیین کند.

مقایسه نمونه ها (بار دیگر تحلیل واریانس)

بررسی و مشاهده فرضیات اساسی یک مدل خطی در ارتباط  با رگرسیون خطی و نیز همبستگی خطی ساده است. اما این مسئله به صورت ذاتی، خصوصاً زمانی که به مقایسه چند نمونه می پردازیم، برقرار نیست (به عنوان مثال در آزمون t یا ANOVA). این فرض را می توان یک بار دیگر با نگاه کردن به دانش عمومی و داده های سن بررسی نمود. این کار را با در نظر گرفتن یک عامل مستقل اندازه گیری شده در تحلیل واریانس انجام داد، به گونه ای که به مقایسه نمرات دانش عمومی در کلاس های مختلف پرداخت (کلاس 1، کلاس 2 و کلاس 3). بدین منظور به جای در نظر گرفتن سن آنها، هر 6 دانش آموزی که در سطحی مشابه روی محور افقی قرار دارند را در یک کلاس قرار می دهیم. اما همان منطقی که در بالا هنگام بررسی سن به کار بردیم هنوز هم صدق می کند. می توان یک طرح از داده ها را در شکل 23.8مشاهده کرد.

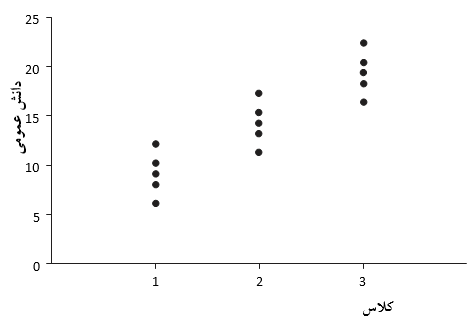
شکل 23.8- نمودار نمرات دانش عمومی در هر کلاس

اکنون می توانیم دقیقاً مشابه همان کاری که با نمودار پراکنش نمرات دانش عمومی و سن انجام دادیم، عمل کنیم. آیا با استفاده از شکل 23.8- می توان متوجه شد که یک مدل خطی وجود دارد؟ اگرچه به طور معمول با فکر کردن در مورد داده های دسته بندی مانند این نمی توان وجود یا عدم وجود و میزان همبستگی را تشخیص

با انجام تحلیل رگرسیون می توانیم بهترین مدل خطی متناسب با این داده ها را پیدا کنیم. نتایج بدست آمده فرمول زیر را به ما می دهد:

Y=4+5X

بنابراین “بهترین برازش” در این مدل خطی به صورت زیر پیش بینی را انجام می دهد:

نمره دانش عمومی = 4 + 5 × کلاس

این مدل در شکل 23-9 نشان داده شده است.

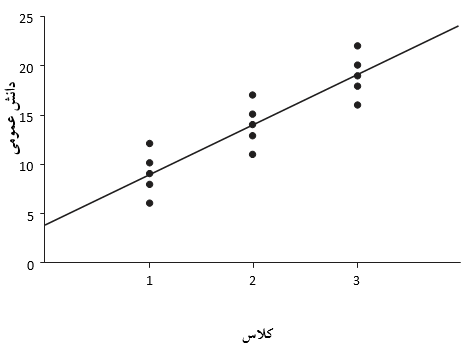
شکل 23-9- مدل خطی برای داده های کلاس بندی شده

نکته جالب قابل برداشت از شکل 23-9 دلیل در نظر گرفتن فرض هم واریانسی حین محاسبه همبستگی است. در واقع فرض می کنیم که داده ها در هر سه کلاس به طور مساوی در اطراف خط رگرسیون پراکنده می شوند.

اکنون که مدل خود را داریم، می توانیم نمرات دانش عمومی را توسط مدل که در حقیقت نوعی پیش بینی از نمرات و باقیمانده ها یا ‘خطا’ها ارائه می دهد، پیش بینی کنیم. توجه کنید که بر اساس ستون سوم جدول زیر، نمرات پیش بینی شده توسط مدل میانگین گروه است، بنابراین نمره پیش بینی شده برای همه دانش آموزان کلاس ،1 میانگین کلاس 1 (نمره 9) است. باقیمانده ها در ستون ششم نشان داده شده اند. درست همانطور که در تحلیل واریانس مورد قبل انجام دادیم، برای پیش بینی شده هر نقطه از داده ها توسط مدل، از فاصله هر داده از میانگین استفاده می کنیم (زیرا این همان میزان تغییری است که مدل قادر به تبیین آن است). سپس این مقادیر را به توان دو رسانده تا معیاری از تغییرات تبیین شده را تولید کنیم. اگر این مقادیر را جمع کنیم، شاخص “مجموع مربعات” برای تغییرات تبیین شده تولید می شود. همچنین باقیمانده ها را نیز به توان دو رسانده تا شاخصی نیز برای بخش تغییرات تبیین نشده بدست آوریم. جمع کردن این مقادیر، “مجموع مربعات” برای تغییرات خطا را به ما می دهد. این موارد نیز در جدول زیر ذکر شده است.

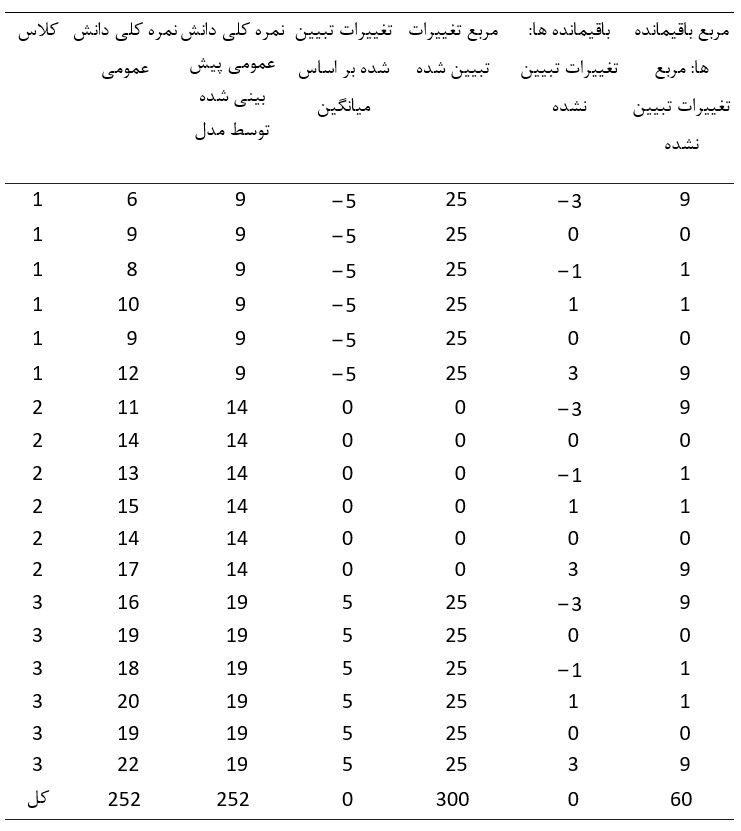
تجزیه و تحلیل داده ها براساس کلاس و نه سن، مجموع مربعات کل (360.00) را به آنچه توسط مدل تبیین شده (300.00) و بخش باقیمانده که مدل آن را توضیح نمی دهد (60.00) تقسیم می کند. واضح است که این مدل می تواند بخش قابل توجهی از تغییرات داده ها را به احتساب آورد (p<0.01). از این رو می توانیم فرض صفر مبنی بر اینکه میانگین توزیع جمعیت ها یکسان است را رد کنیم.

تبیین تغییرات داده ها

شاید از خود پرسیده باشید که چرا در هر دو تحلیل واریانس فوق، تغییرات تبیین شده در داده ها را نسبت به مقدار میانگین بررسی کردیم. پاسخ از نحوه محاسبه تغییراتِ داده ها ناشی می شود. اگر نمرات دانش عمومی را به توان دو برسانیم و آنها را جمع کنیم، مقدار 3888 حاصل می شود.

این مقدار تنها درصورتی می تواند به عنوان معیار کل تغییرات داده ها محسوب شود که میانگین برابر با صفر باشد.

دو نمره 99 و 101 را در نظر بگیرید. تفاوت این نمره ها مقدار 2 است، به گونه ای که عدد 99 یک واحد زیر میانگین، یعنی عدد 100 است و عدد 101 یک واحد بالاتر از میانگین 100 است. اکنون دو نمره دیگر یعنی 25 و 35 را در نظر بگیرید. تفاضل این اعداد برابر با ده است و عدد 25، پنج واحد کمتر از میانگین این اعداد یعنی 30 است، در حالیکه عدد 35، پنج واحد بالاتر از میانگین یعنی عدد 30 است. در مقایسه این دو جفت اعداد متوجه می شویم اگرچه اعداد 25 و 35 کوچکتر از 99 و 101 هستند، ولی تغییرات بیشتری نسبت به اعداد سری اول دارند. بنابراین هنگام بررسی تغییرات داده ها ما به مقادیر واقعی آنها علاقه مند نیستیم و این میزان تغییرات بین آنها است که برای ما مهم است، از این لحاظ است که اعداد بر اساس میانگین هایشان مقایسه می شوند. بعضی اوقات در خروجی برنامه های آماری کامپیوتری می بینید که مجموع مربعات نمرات به عنوان “کل” و مجموع مربعات نمرات منهای میانگین به عنوان “کل اصلاح شده” به عنوان دومین شاخص استخراج شده از میزان تغییرات داده ها که به نوعی اصلاح شده است را به ما می دهد. در مثال ما مجموع اصلاح شده 360 است (مقداری که در محاسبات فوق به عنوان کل تغییرات داده ها استفاده کردیم). تفاوت بین کل و کل تصحیح شده، 3888-360=3528 به سادگی نشان می دهد که تفاوت مقدار میانگین از صفر چقدر است.

تا اینجا دو تحلیل واریانس را در ارتباط با نمرات دانش عمومی انجام داده ایم. اولین تحلیل، رابطه میان نمرات دانش عمومی و سن را بررسی کرد و دومین مورد گروه دوم نمرات دانش عمومی را در سه کلاس مقایسه کرد. در هر دو مورد، تجزیه و تحلیل فقط به این دلیل امکان پذیر بود که ما یک مدل خطی را برای داده ها فرض کرده بودیم. مدل هایی که به بهترین شکل ممکن متناسب با داده ها بودند، در دو مورد متفاوت بودند؛ زیرا اولین تحلیل شامل اطلاعات مربوط به سن بود در حالی که مورد دوم فقط شامل اطلاعات کلاس بود. در هر صورت با توجه به اینکه تجزیه و تحلیل در مورد بررسی تبین تغییرات در نمرات دانش عمومی انجام شده است، تعجب آور نیست که ببینیم تغییرات کلی در داده ها (“مجموع مربعات”) در هر دو حالت مقدار 360 را به خود اختصاص داده است. با فرض خطی بودن مدل، توانستیم تغییرات کل را به “تغییرات تبیین شده توسط مدل” و تغییرات غیرقابل تبیین در داده ها تفکیک کنیم. در اولین تجزیه و تحلیل، “مجموع مربعات تبیین شده برابر با ” 342.29 و “مجموع مربعات  تبیین نشده” مقدار 17.71 را به خود اختصاص داده بود. در تحلیل دوم این مقادیر به ترتیب برابر با 300 و 60 بدست آمدند.

مدل خطی عام

تا کنون با ساده ترین حالت مدل خطی سروکار داشتیم، یعنی یک رابطه مستقیم بین دو متغیر، که با فرمول Y = a + bX نشان داده شد. در حقیقت این مدل ساده ترین حالت مدل عام است که فقط شامل یک متغیر مستقل یا همان X می شود، ولی مدلهای کلی تری نیز وجود دارند که می توانند تعداد زیادی متغیر مستقل در بر داشته باشند (در واقع در فصل 15 شاهد یک ANOVA دو عاملی به عنوان دو متغیر مستقل بودیم). علاوه بر این، این کار را همچنین می توان برای چندین متغیر وابسته یا  Y انجام داد. برای نشان دادن این موضوع ابتدا باید مدل خود را به صورت ماتریسی نمایش دهیم.

نمایش ماتریسی برای مثالهای انجام شده شامل دو متغیر

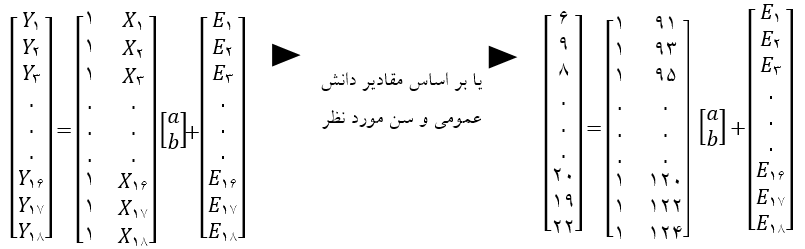
یک بار دیگر مثال دانش عمومی و سنی را در نظر بگیرید. برای یافتن مدل خطی، خطای Y = a + bX + E را به حداقل می رسانیم، که در آن Y نمره آزمون است، X سن و E خطا یا باقیمانده است. بنابراین می توانیم برای هر کدام از دانش آموزان نمرات آنها را یک به یک در فرمول قرار دهیم:

(من از نقاط کوچک برای نشان دادن بقیه مقادیری که می بایست در اینجا گنجانده شود، استفاده کرده زیرا در غیر این صورت مجبور بودم فرمول مذکور را برای تمامی هجده دانش آموز لیست کنم.)

اجزای ماتریس را به صورت زیر می توان نشان داد:

می توان از حروف بزرگ و پررنگ برای نشان دادن ماتریس ها به جای حروف کوچکتر که برای نشان دادن مقادیر درون ماتریسها به کار بردیم، استفاده کرد. بنابراین ماتریس ها را به صورت می توان زیر جایگزین نمود:

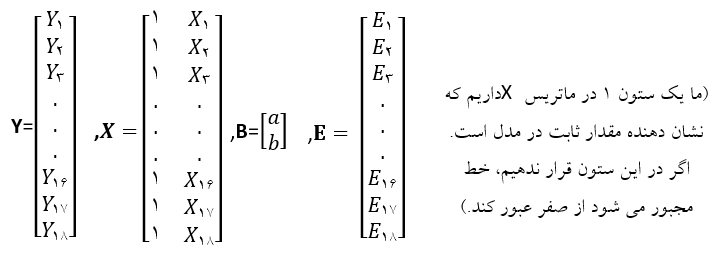
بنابراین بر اساس اصطلاحات ماتریسی خواهیم داشت:

با بکارگیری جبر ماتریسها (که تا حدودی پیچیده و خارج از سطح این کتاب است) می توان با مینیمم ساختن خطا مقادیر “a” و “b” را بدست آورد. داریم

که در آن  ترانهاده  و با جابجایی سطرها و ستون های ماتریس  حاصل می شود، همچنین ماتریس معکوس (که به صورت ماتریس به توان -1 نمایش داده می شود) را می توان با یک فرمول ریاضی محاسبه کرد.

اکنون می توانیم با استفاده از اطلاعاتی که در دست داریم و نیز با استفاده از جبر ماتریس ها (که انتظار ندارم از آن بدانید) مقادیر مناسب برای “a” و “b” را بدست آوریم. لذا داریم:

.

امیدوارم حتی برای خوانندگانی که با جبر ماتریس ها آشنا نیستند، تمام آنچه که ما انجام داده ایم واضح باشد. در حقیقت این کار نمایش دیگری از همان مدل اما به روشی متفاوت است.

متغیرهای  چندگانه X

با داشتن بیش از دو متغیر می توانیم مدل خطی را گسترش دهیم. اگر به فصل 21 مربوط به رگرسیون چندگانه مراجعه کنید، مشاهده می شود که فرمولی که به کار می بریم به شکل زیر است:

Y=a+b1X1+b2X2+b3X3+…

این مدل هنوز یک مدل خطی است زیرا همچنان شامل مقدار ثابت “a” به علاوه شیب “b” است، اما در اینجا برای هر یک از متغیرهای X مقدار b داریم. اساساً مدل خطی بدین معنی است که مقادیر توان دو یا بالاتر از X در فرمول وجود ندارد. تا اینجای کار ما فقط با دو متغیر کار کردیم که حاصل آن یک خط مستقیم در فضای دو بعدی بود، در حالیکه در این بخش مدل خطی دیگر یک خط مستقیم نیست بلکه یک فضای چند بعدی است. اما می توانیم از همان منطق استفاده کنیم تا هر تعداد متغیر مستقل یا X را در تجزیه و تحلیل مورد نظر خود بررسی کنیم و همبستگی و رگرسیون چندگانه را علاوه بر تحلیل واریانس چند عاملی اعمال کنیم؛ به عنوان مثال می توانیم تحلیل واریانس دو عاملی را انجام دهیم.

چنانچه اشاره شد این مدل هنوز یک مدل خطی به شکل زیر است:

 Y = XB + E

در این حالت ماتریس X به شکل زیر نمایش داده می شود

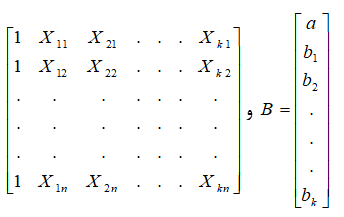
که در آن n تعداد شرکت کنندگان و k تعداد متغیرهای مستقل است، به عنوان مثال ،  مقدار شرکت کننده 2 در اولین متغیر مستقل است.

مدل خطی عام و تحلیل چند متغیره

دقیقا مشابه آنچه که برای متغیرهای مستقل X انجام دادیم، می توانیم مدل خطی را برای بیش از یک متغیر وابسته Y تعمیم دهیم. این تحلیل را که مستلزم چندین متغیر وابسته است را تحلیل چند متغیره (multivariate analysis) می نامیم و در مقابل حالتی با فقط یک متغیر وابسته تحلیل یک متغیره نامیده می شود (univariate analysis) (همانطور که در فصل 22 مشاهده کردیم). اما نوشتار ماتریس تغییر نمی کند و همچنان داریم:

Y=XB+E

اما در این حالت ماتریس Y به صورت زیر است

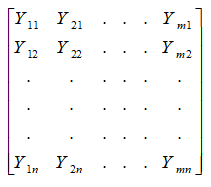
که در آن m تعداد متغیرهای وابسته است و به عنوان مثال نمره اولین شرکت کننده در متغیر وابسته دوم است. این مدل به عنوان مدل خطی عام شناخته می شود زیرا می تواند شامل چندین متغیر وابسته مستقل باشد. در فصل 22 نیز با تحلیل چند متغیره سر و کار داشتیم و ماتریس هایی  در تحلیل های پیچیده معرفی و مطرح شدند (مانند تحلیل عاملی و تحلیل واریانس چند متغیره).

نکته مهم در اینجا این است که صرف نظر از اینکه ما با یک متغیر مستقل و یک متغیر وابسته سروکار داریم یا تعداد زیادی از آنها، تا زمانی که مفروضات مد نظر برقرار باشند می توانیم داده های خود را بر روی یک مدل خطی تصویر کنیم و در حقیقت ابزاری قدرتمند برای ایجاد محک زدن یافته های تحقیق داریم. همانطور که دانشمندان از مدلهای منظومه شمسی خود برای پیش بینی حرکت سیارات استفاده می کنند، ما نیز می توانیم از یک مدل خطی برای پیش بینی روابط بین متغیرهایی که داریم استفاده کنیم. ممکن است از احتمال کاوش در سیارات دیگر هیجان زده شویم، اما ابتدا باید با خیال راحت به آنجا برویم و فقط با یک مدل خوب می توانیم این کار را انجام دهیم. به همین ترتیب، ممکن است بخواهیم روابط جالب بین متغیرها را در زمینه مطالعه خود کشف کنیم و اینجاست که نقش مدل خطی عام در فرآیند های تجزیه و تحلیل داده های کمی ستودنی است، به گونه ای که کمک شایانی در کمک به ما برای نتیجه گیری از مطالعاتمان دارد.

امیدوارم این شرح مختصر از مدل خطی عام در تجزیه و تحلیل آماری، بینشی در مورد ساخت و کاربرد بسیاری از آزمونهای آماری داده باشد. به ویژه آگاهی از اهمیت باقیمانده ها برای درک مفروضات مورد نیاز این آزمون ها بسیار مهم است. به هر حال توضیح بیشتر مستلزم ورود عمیق تری به جبر ماتریس ها است که از حوصله این کتاب خارج است.

مترجمین: دکتر هدی کامرانی فر – حسن اسکندری نیا