استفاده از ابزار Solver برای حل مشکلات مربوط به نقل‌ و انتقال و توزیع

آخرین به‌روزرسانی: 27 دی 1401

در سری مقاله های آموزش اکسل، در فصل گذشته به استفاده از ابزار Solver برای برنامه ریزی زمان‌بندی نیروی کار پرداختیم، در این مقاله “استفاده از ابزار Solver برای حل مشکلات مربوط به نقل‌ و انتقال و توزیع” را مورد بررسی قرار می‌دهیم.

بسیاری از شرکت‌ها محصولات خود را در مکان‌های مختلفی تولید (که اغلب آنها را مراکز عرضه می‌نامند) و یا به مشتریان ارسال می‌کنند (که اغلب آنها را مراکز تقاضا می‌نامند). سؤالی که به طور طبیعی به وجود می‌آید آن است که” ارزان‌ترین راه برای تولید و ارسال محصولات به مشتریان که درعین‌حال بتواند پاسخگوی تقاضاهای موجود نیز باشد کدام است؟

تولید و توزیع دارو با استفاده از ابزار Solver

” این نوع از مسائل، مسئله‌های نقل‌وانتقال نامیده می‌شود. برای یک مسئله نقل‌وانتقال می‌توان مدل Solver خطی با مشخصه‌های زیر ایجاد کرد:

• سلول هدف تولید کل و هزینه ارسال را به حداقل می‌رساند.
• سلول‌های متغیر عبارت‌اند از میزان محصولات در هر مرکز عرضه که به مراکز تقاضا ارسال می‌شوند.
• محدودیت‌ها مشخص می‌کنند که میزان محصول ارسال شده از هر مرکز عرضه نمی‌بایست از ظرفیت کارخانه بیشتر شوند. هر مرکز تقاضا می‌بایست تنها میزان تقاضای مورد نیازش را دریافت کند. همچنین مقدار هر سلول متغیر نمی‌بایست عدد منفی باشد.

یک شرکت داروسازی چگونه می‌تواند مشخص کند داروهایش را در کدام‌ یک از مکان‌های موجود تولید کند و از کدام مکان آنها را به مشتریان ارسال نماید؟

می‌توانید این مسئله را با نگاه به فایل Transport.xlsx دنبال کنید. بیایید فرض کنیم شرکتی در تأسیساتی در لس‌آنجلس، آتلانتا و نیویورک میزان معینی دارو تولید می‌کند. کارخانه لس‌آنجلس می‌تواند هر ماه تا 10000 پوند از آن دارو تولید کند. کارخانه آتلانتا می‌تواند تا 12000 پوند دارو و کارخانه نیویورک می‌تواند تا 14000 پوند از آن دارو تولید کند. کارخانه هر ماه می‌بایست تعداد پوندهای فهرست شده در سلول‌های B2:E2 را همان‌طور که در تصویر 1-32 نشان‌داده‌شده، به چهار منطقه در ایالات متحده (شرق، غرب میانه، جنوب و غرب) ارسال کند. مثلاً منطقه غرب می‌بایست ماهیانه حداقل 13000 پوند از آن دارو را دریافت کند. هزینه هر پوند تولید دارو در هر کارخانه و ارسال دارو به مناطق کشور در سلول‌های B4:E6 قرار داده شده است. مثلاً تولید یک پوند از دارو در لس‌آنجلس و ارسال آن به منطقه غرب میانه3.50 دلار هزینه صرف می‌کند. ارزان‌ترین راه برای رساندن داروی موردنیاز برای هر منطقه کدام است؟

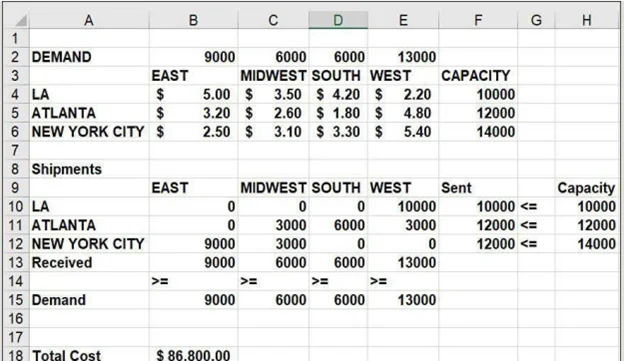
تصویر 1-32 داده‌های مسئله نقل‌وانتقال

برای نمایش سلول هدف می‌بایست هزینه کل ارسال را دنبال نمایید. پس از واردکردن مقادیر آزمایشی برای ارسال از هر نقطه عرضه به هر منطقه در محدوده سلول B10:E12 می‌توانید هزینه ارسال کل را به شکل زیر محاسبه کنید:

(میزان فرستاده شده از لس‌آنجلس به شرق)*(هزینه هر پوند داروی ارسال شده از لس‌آنجلس به شرق)+ (میزان فرستاده شده از لس‌آنجلس به غرب میانه)*(هزینه هر پوند داروی ارسال شده از لس‌آنجلس به غرب میانه)+ (میزان فرستاده شده از لس‌آنجلس به جنوب)*(هزینه هر پوند داروی ارسال شده از لس‌آنجلس به جنوب)+ (میزان فرستاده شده از لس‌آنجلس به غرب)*(هزینه هر پوند داروی ارسال شده از لس‌آنجلس به غرب)+ … (میزان فرستاده شده از نیویورک سیتی به غرب)*(هزینه هر پوند داروی ارسال شده از نیویورک سیتی به غرب)

تابع SUMPRODUCT می‌تواند عناصر مربوطه در دو کادر مستطیلی جداگانه را درهم ضرب کند (تا وقتی که مستطیل‌ها در یک اندازه باشند) و محصولات را به آن اضافه نماید. ما محدوده سلولی B4:E6 را هزینه‌ها (Costs) و محدوده سلول متغیر (B10:E12) را ارسال شده (Shipped) می‌نامیم.

بنابراین هزینه کل ارسال و تولید در سلول B18 با فرمول =SUMPRODUCT(costs,shipped) محاسبه می‌گردد.

برای ایجاد محدودیت این مسئله، ابتدا کل کالاهای ارسال شده را از نقطه ارسال محاسبه می‌کنیم. با واردکردن فرمول =SUM(B10:E10) در سلول F10 تعداد کل پوندهای ارسال شده از لوس آنجلس را به این شکل: (موارد ارسال شده از لوس آنجلس به شرق) +(موارد ارسال شده از لوس آنجلس به غرب میانه)+ (موارد ارسال شده از لوس آنجلس به جنوب)+ (موارد ارسال شده از لوس آنجلس به غرب) محاسبه می‌کنیم. کپی‌کردن این فرمول به محدوده F11:F12 کل موارد ارسال شده از آتلانتا و نیویورک سیتی را محاسبه می‌کند. پس از آن یک محدودیت (به نام محدودیت عرضه) اضافه می‌کنیم تا اطمینان حاصل نماییم که میزان ارسال شده از هر موقعیت مکانی از ظرفیت کارخانه بالاتر نباشد.

سپس مقدار کل کالاهای دریافت شده توسط هر نقطه تقاضا را محاسبه می‌کنیم. کار را با وارد نمودن فرمول =SUM(B10:B12) در سلول B13 آغاز می‌کنیم. این فرمول مقدار کل پوندهای محصول دریافت شده در شرق را به شکل: (پوندهای ارسال شده از لس‌آنجلس به شرق)+(پوندهای ارسال شده از آتلانتا به شرق) + (تعداد پوندهای ارسال شده از نیویورک سیتی به شرق) محاسبه می‌کند. با کپی‌کردن این فرمول از سلول B13 به محدوده C13:E13 تعداد پوندهای داروی دریافت شده در غرب میانه، جنوب، و غرب را محاسبه می‌کنیم. پس از آن محدودیتی (به نام محدودیت تقاضا) اضافه می‌کنیم که به ما اطمینان می‌دهد که هر منطقه میزان داروهای مورد نیازش را دریافت نموده است.

حالا کادر محاوره‌ای Solver Parameters را باز می‌کنیم (بر روی گزینه Solver در گروه گزینه‌های Analyze در تب Data کلیک می‌کنیم) و آن را همانند تصویر 2-32 پر می‌کنیم.

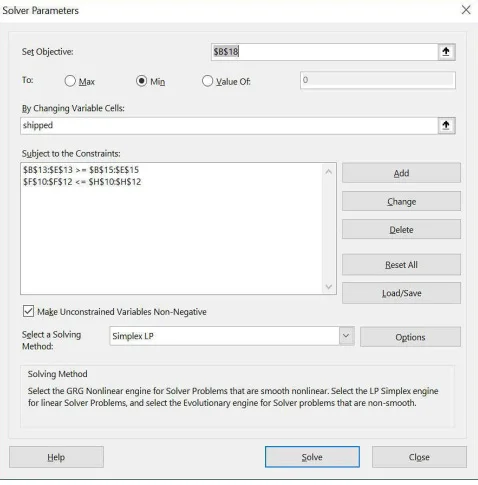
تصویر 2-32 تنظیم Solver برای حل مسئله نقل‌وانتقال

قصد داریم که هزینه ارسال را (که در سلول B18 محاسبه شده) کم کنیم. سلول‌های متغیر تعداد پوندهایی از محصولات هستند که از هر کارخانه به مناطق مختلف کشور ارسال شده‌اند (این مقادیر در محدوده‌ای به نام Shipped که شامل سلول‌های B10:E12 هستند ذخیره شده‌اند) فرمول محدودیت F10:F12<=H10:H12 (محدودیت عرضه) به ما اطمینان می‌دهد که مقادیر فرستاده شده از هر کارخانه بیشتر ظرفیت آن نمی‌باشد. فرمول محدودیت B13:E13>=B15:E15 (محدودیت تقاضا) به ما اطمینان می‌دهد که هر منطقه دست‌کم میزان داروی مورد نیازش را دریافت می‌کند. این مدل یک مدل Solver خطی است، چرا که سلول هدف با اضافه‌کردن شرایط شکل (سلول متغیر)*(محدودیت) به وجود آمده و هر دو محدودیت‌های عرضه و تقاضا با استفاده از مقایسه سلول‌های متغیر با یک محدودیت به‌دست‌آمده‌اند. ازآنجاکه مدل خطی است، موتور Simplex LP را انتخاب می‌کنیم. مشخص است که مقادیر ارسال می‌بایست اعدادی غیرمنفی باشند، بنابراین چک باکس Make Unconstrained Variable Non- Negative را انتخاب می‌کنیم.

پس از کلیک کردن بر روی دکمه Solver در کادر محاوره‌ای Solver Parameters،راه‌حل بهینه‌ای برای مشکل موردنظر که در تصویر 1-32 نشان‌داده‌شده به ما ارائه می‌شود. حداقل هزینه برای برآورده کردن تقاضای مشتریان 86.800 دلار است. این حداقل هزینه را درصورتی‌که کارخانه از برنامه تولید و ارسال زیر استفاده کند می‌توان به دست آورد.

• 10000 پوند محصول از لس‌آنجلس به غرب میانه ارسال شود.
• 3000 پوند محصول از آتلانتا به غرب ارسال شده و همان مقدار نیز از آتلانتا به غرب میانه ارسال گردد.6000 پوند نیز از آتلانتا به جنوب ارسال گردد.
• 9000 پوند از نیویورک سیتی به شرق ارسال و 3000 پوند نیز از نیویورک سیتی به غرب میانه ارسال گردد.

مسئله‌های این فصل:

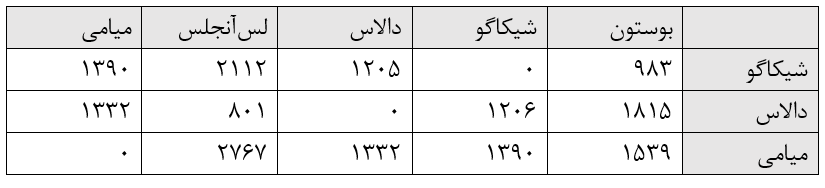
جدول زیر فواصل میان بوستون، شیکاگو، دالاس، لس‌آنجلس و میامی را نشان می‌دهد. هر شهر نیازمند 40000 کیلووات بر ساعت برق است و شهرهای شیکاگو، دالاس و میامی قادر به تولید 70000 کیلووات بر ساعت برق هستند. فرض کنید ارسال 1000 کیلووات بر ساعت برق به فاصله 100 مایل 4 دلار هزینه صرف می‌کند. برق از کجا می‌بایست ارسال شود تا برآورده کردن تقاضای هر شهر با حداقل هزینه ممکن انجام شود؟

مسئله ارائه شده در این فصل را به فرض به اینکه میزان تقاضا در منطقه غرب به 13000 افزایش پیدا کرده حل کنید.

شرکتی داروهایی را در مناطق مختلفی تولید و به فروش می‌رساند. تصمیم‌گیری مکان تولید محصولات برای هریک از مناطق تولید می‌تواند اثر بسیار بالایی روی سود شرکت داشته باشد. مدلی که در اینجا وجود دارد شبیه مدلی است که در همین فصل برای تشخیص اینکه داروها در چه مکانی تولید شود مورداستفاده قرار گرفت. از فرض‌های زیر برای حل این مسئله استفاده کنید.

1. داروها در شش مکان مختلف تولید و در شش مکان مختلف به مصرف‌کنندگان فروخته می‌شوند.
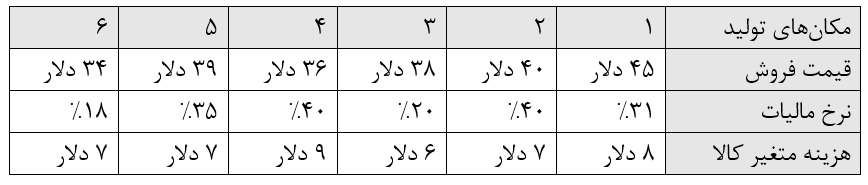
2. نرخ مالیات و هزینه متغیر محصولات بستگی که مکانی که محصولات تولید می‌شوند دارد. مثلاً هر واحد از تولید در مکان شماره 3 به میزان 3 دلار هزینه تولید دارد، به سود ناشی از این محصولات 20 درصد مالیات تعلق می‌گیرد.
3. قیمت فروش هریک از داروها بستگی به مکانی که دارو در آنجا تولید می‌شود دارد. مثلاً هر محصول در مکان شماره 2 به قیمت 40 دلار فروخته می‌شود.

4.هریک از شش کارخانه می‌توانند سالیانه 6 میلیون واحد تولید کنند.

5.تقاضای سالیانه (به میلیون) برای محصولات در هر یک از مناطق در جدول زیر ارائه شده:

6.هزینه ارسال محصولات همان‌طور که در این جدول می‌بینید، بستگی به جایی که محصول تولید می‌شود و همچنین مکانی که در آن به فروش می‌رسد دارد

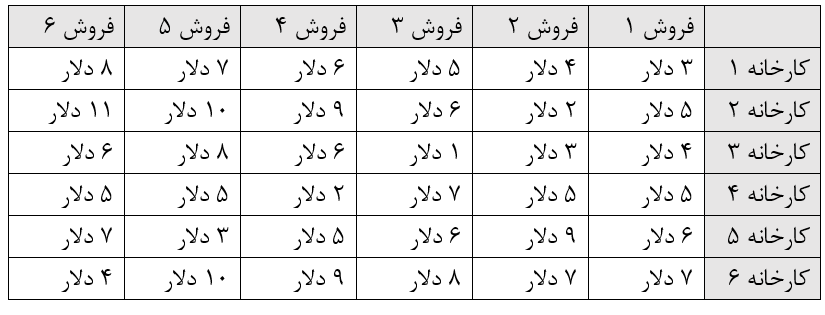
مثلاً اگر واحدی در کارخانه 1 تولید و در منطقه شماره 3 فروخته شود، برای ارسال آن می‌بایست 5 دلار هزینه شود. چگونه می‌توان سود پس از مالیات را با وجود ظرفیت تولید محدود افزایش داد؟

فرض کنید که بخش‌های شمالی، مرکزی و جنوبی کالیفرنیا هرکدام روزانه 100 میلیارد گالن آب مصرف می‌کنند. همچنین در نظر داشته باشید که کالیفرنیای شمالی و مرکزی 120 میلیارد گالن آب در اختیار دارند درحالی‌که کالیفرنیایی جنوبی 40 میلیارد گالن آب در اختیار دارد. هزینه ارسال 1 میلیارد گالن آب بین این سه منطقه در جدول زیر ارائه شده است:

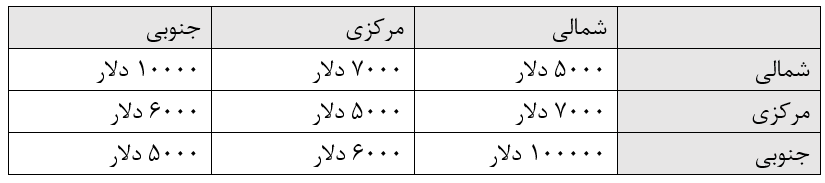
شما قادر نخواهید بود تا تمامی تقاضاهای آب را برآورده کنید، بنابراین فرض کنید که هر میلیارد گالن تقاضای برآورده نشده هزینه‌های کمبود زیر را متحمل خواهد کرد:

آب کالیفرنیا چگونه می‌بایست توزیع شود تا مجموع هزینه‌های ارسال و کمبود به حداقل برسد؟

یک فروشگاه ابزارفروشی در هریک از انبارهای هیوستون، دالاس و سان آنتونیو دارای 50 ماشین علف‌چین است. این ماه قرار است 35 ماشین علف‌چین در هیوستون، دالاس، سان آنتونیو و آستن فروخته شوند. هزینه ارسال یک ماشین علف‌چین از انبار به هریک از شهرها در زیر نشان‌داده‌شده. تعیین کنید چگونه می‌توان تقاضا را با حداقل هزینه برآورده نمود. (تصویر 3.23 را ببینید)

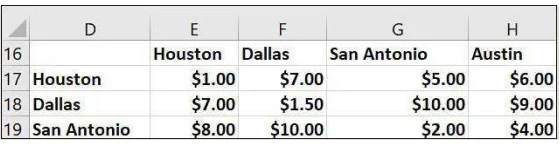
تصویر 3-32 داده‌های مسئله شماره 5

چگونه می‌توان از آیکون AutoSum برای کمک به حل مسئله‌های حمل‌ونقل استفاده کرد؟